VECTORES

 http://genesis.uag.mx/edmedia/material/fisica/vectores1.htm 
http://www.monografias.com/trabajos35/vectores/vectores.shtml
Definición de vectores
Un vector es todo segmento de recta dirigido en el espacio. Cada vector posee unas características que son:
Origen
O también denominado Punto de aplicación. Es el punto exacto sobre el que actúa el vector.
Módulo
Es la longitud o tamaño del vector. Para hallarla es preciso conocer el origen y el extremo del vector, pues para saber cuál es el módulo del vector, debemos medir desde su origen hasta su extremo.
Dirección
Viene dada por la orientación en el espacio de la recta que lo contiene.
Sentido
Se indica mediante una punta de flecha situada en el extremo del vector, indicando hacia qué lado de la línea de acción se dirige el vector.
Hay que tener muy en cuenta el sistema de referencia de los vectores, que estará formado por un origen y tres ejes perpendiculares. Este sistema de referencia permite fijar la posición de un punto cualquiera con exactitud.
El sistema de referencia que usaremos, como norma general, es el Sistema de Coordenadas Cartesianas.

Para poder representar cada vector en este sistema de coordenadas cartesianas, haremos uso de tres vectores unitarios. Estos vectores unitarios, son unidimensionales, esto es, tienen módulo 1, son perpendiculares entre sí y corresponderán a cada uno de los ejes del sistema de referencia.

Magnitudes Escalares
Denominamos Magnitudes Escalares a aquellas en las que las medidas quedan correctamente expresadas por medio de un número y la correspondiente unidad. Ejemplo de ello son las siguientes magnitudes, entre otras:
Masa
Temperatura
Presión
Densidad
Magnitudes vectoriales
Las magnitudes vectoriales son magnitudes que para estar determinadas precisan de un valor numérico, una dirección, un sentido y un punto de aplicación.
Vector
Un vector es la expresión que proporciona la medida de cualquier magnitud vectorial. Podemos considerarlo como un segmento orientado, en el que cabe distinguir:

• Un origen o punto de aplicación: A.
• Un extremo: B.
• Una dirección: la de la recta que lo contiene.
• Un sentido: indicado por la punta de flecha en B.
• Un módulo, indicativo de la longitud del segmento AB.

Vectores iguales
Dos vectores son iguales cuando tienen el mismo módulo y la misma dirección.
Vector libre
Un vector libre queda caracterizado por su módulo, dirección y sentido. El vector libre es independiente del lugar en el que se encuentra.
Descomponiendo en un sistema de ejes cartesianos
a+b=(axi+ayj+ azk)+(bxi+byj+ bzk)=(ax+bx)i+(ay +by)j+(az+bz)k

Propiedades
Conmutativa: a+b=b+a
Asociativa: (a+b)+c=a+(b+c)
Elemento Neutro: a+0=a
Elemento Simétrico: a+(-a)=a-a=0
Vectores unitarios y componentes de un vector
Cualquier vector puede ser considerado como resultado de la suma de tres vectores, cada uno de ellos en la dirección de uno de los ejes coordenados.

Suma y resta de vectores
La suma de dos vectores libres es otro vector libre que se determina de la siguiente forma:
Se sitúa el punto de aplicación de uno de ellos sobre el extremo del otro; el vector suma es el vector que tiene su origen en el origen del primero y su extremo en el extremo del segundo.
Por tanto, el vector suma de dos vectores coincide con una de las diagonales, la "saliente", del paralelogramo que puede formarse con los vectores que se suman; la otra diagonal representa la resta de dichos vectores.

Para efectuar sumas o restas de tres o más vectores, el proceso es idéntico. Basta con aplicar la propiedad asociativa.
Al vector que se obtiene al sumar o restar varios vectores se le denomina resultante.
Suma de Vectores
La suma de los vectores podemos realizarla de dos maneras diferentes, analítica y gráficamente.
Procedimiento Gráfico
Para sumar dos vectores de manera gráfica utilizaremos la denominada Regla del paralelogramo, consistente en trasladar paralelamente los vectores hasta unirlos por el origen, y luego trazar un paralelogramo, del que obtendremos el resultado de la suma, como consecuencia de dibujar la diagonal de ese paralelogramo, como podemos ver en el siguiente dibujo:

Otra manera de expresar la suma de manera gráfica es trasladar el segundo vector a sumar de tal manera que el origen de éste, coincida con el extremo del primer vector, y la suma la obtendremos dibujando un vector que vaya desde el origen del primer vector hasta el extremo del segundo, de la siguiente manera:

Hay que tener muy presente lo siguiente: vectores en la misma dirección se suman (tal y como ya hemos visto en la sección de la suma de vectores), pero vectores con sentidos opuestos se restan (tal y como se puede ver en el apartado correspondiente a la resta de vectores). A continuación tenemos un ejemplo de suma y resta de vectores.

 

Método Algebraico para la Suma de vectores
Dados tres vectores

La expresión correspondiente al vector suma es:

o bien

siendo, por tanto,

La suma de vectores goza de las siguientes propiedades:
Conmutativa
a + b = b + a
Asociativa
(a + b) + c = a + (b + c)
Elemento neutro o vector 0
a + 0 = 0 + a = a
Elemento simétrico u opuesto a'
a + a' = a' + a = 0
a' = -a
Producto de un vector por un escalar
El resultado de multiplicar un escalar k por un vector v, expresado analíticamente por kv, es otro vector con las siguientes características :
1.- Tiene la misma dirección que v.
2.- Su sentido coincide con el de v, si k es un número positivo, y es el opuesto, si k es un número negativo.
3.- El módulo es k veces la longitud que representa el módulo de v. ( Si k es 0 el resultado es el vector nulo).
Analíticamente, tenemos que multiplicar el escalar por cada una de las coordenadas del vector.
Ejemplo : Dado el vector v de componentes : vxi + vyj + vzk, el producto 3 · v = 3 · vxi + 3 · vyj + 3 · vzk.
La representación gráfica del producto es igual a sumar el vector tantas veces como indica el escalar.
Ejemplo :

Propiedades
El producto de un vector por un escalar cumple las siguientes propiedades:

Producto escalar de dos vectores
El producto escalar de dos vectores, expresado analíticamente como r · v, se obtiene de la suma de los productos formados por las componentes de uno y otro vector. Es decir, dados dos vectores r y v, expresados en un mismo sistema de coordenadas:
r = rxi + ryj + rzk
v = vxi + vyj + vzk
teniendo en cuenta que el producto escalar de los vectores :
i · i = j · j = k · k = 1
i · j = i · k = j · k = 0
el resultado de multiplicar escalarmente r por v es:
r · v = rx· vx + ry · vy+ rz · vz
Esta operación no solo nos permite el cálculo de la longitud de los segmentos orientados que representan ( sus módulos ), sino también calcular el ángulo que hay entre ellos. Esto es posible, ya que el producto escalar también se puede hallar en función de sus módulos y del coseno del ángulo que forman mediante la fórmula :
r · v = |r| · |v| · cos (r, v)
Propiedades
Conmutativa : r · v = v · r
Distributiva : r · ( v + u ) = r · v + r · uAsociativa : ( k · r ) · v = k · ( r · v ) = r · ( k · v ) siendo k escalar.
Además :
1.- r · r = 0 si, y sólo sí r = 0.
2.- Si r y v <> 0 y r · v = 0, esto implica que los vectores son perpendiculares, (cos 90º = 0).
3.- El producto escalar de dos vectores es equivalente a multiplicar escalarmente uno de ellos por el vector proyección del otro sobre él.
Ejemplo :
Proyección ortogonal (rv) de r sobre v
rv= |r| cos (r, v) -> r · v = |v| · rv
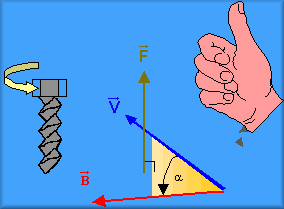
Producto vectorial
El producto vectorial de los vectores a y b, se define como un vector, donde su dirección es perpendicular al plano de a y b, en el sentido del movimiento de un tornillo que gira hacia la derecha por el camino más corto de a a b,

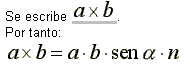
donde n es un vector unitario perpendicular al plano de a y b en el sentido del movimiento de un tornillo que gira hacia la derecha de a a b.
Propiedades:

Módulo de un vector
Un vector no solo nos da una dirección y un sentido, sino también una magnitud, a esa magnitud se le denomina módulo.
Gráficamente: es la distancia que existe entre su origen y su extremo, y se representa por:

Coordenadas cartesianas: En muchas ocasiones es conveniente tomar las componentes sobre tres direcciones mutuamente perpendiculares OX, OY y OZ que forman un sistema cartesiano tridimensional.
Si tomamos tres vectores unitarios, i sobre OX, j sobre OY y k sobre OZ, entonces podemos encontrar puntos ax, ay, az sobre OX, OY, OZ, respectivamente, tales que:

y aplicando el teorema de Pitágoras nos encontramos con que el módulo de a es:

III. Ecuación De La Recta.
Ecuación de la Recta Que Pasa Por El Origen
Considere la recta l que pasa por el origen 0 y forma un ángulo de inclinación con el eje x

Tómese sobre la recta los puntos P1(x1, y1),P2 (x2, y2) y P3 (x3, y3). Al proyectar los puntos P1, P2 y P3 sobre el eje x, se obtienen los puntos P’1, P’2, P’3.
Como los triángulos OP1P’1, OP2P’2 y OP3P’3 son semejantes; se tiene que:

Esto es, cualquiera que sea el punto P(x, y) sobre l, ó y = mx (1)
La ecuación (1) es la ecuación de la recta que pasa por el origen y tiene pendiente conocida m.
Ecuación De La Recta Conocida Su Pendiente m Y Su Intercepto b Con El Eje y
Considere una recta l de la que se conocen m (m = tan ) y b

Trácese por el origen la recta l’ paralela a l. Sea P(x, y) un punto de l. Al  llamar P’ la proyección de P sobre el eje x; PP’ corta a la recta l’ en un punto P’’ de coordenadas

La ecuación y = mx + b es la ecuación de la recta en términos de su pendiente m y su intercepto b con el eje y.
Ecuación De La Recta Que Pasa Por Un Punto Y De Pendiente Conocida
Considere la recta l que pasa por un punto dado P1(x1, y1) y cuya pendiente m también es conocida

..

Al llamar b al intercepto de la recta l con el eje y, entonces la ecuación de l, viene dada por:
                y = mx + b             (1)
Como P1(x1, y1) , entonces satisface (1) y en consecuencia se tiene:

                 y1 = mx1 + b          (2)

Al restar de la ecuación (2) la ecuación (1) se elimina el parámetro b que se desconoce y se obtiene:
y – y1 = m(x – x1) (3)
La ecuación (3) es conocida como la forma: PUNTO-PENDIENTE de la ecuación de la recta.
Nótese que la ecuación (3) también puede escribirse en la forma:
y = mx + (y1 – mx1).
Lo que indica que él intercepto b con el eje y viene dado por:

b = y1 – mx1

Ecuación de la recta que pasa por dos puntos dados P1(x1, y1) y P2(x2, y2)
.. Sea l la recta que pasa por los puntos P1(x1, y1) y P2(x2, y2) y llámese m1 su pendiente

Como l pasa por el punto P1(x1, y1) y tiene pendiente m1, se tiene de acuerdo a 4.4.3, que
                           y – y1 = m1 (x – x1)    (1)
representa la ecuación de dicha recta.
Ahora, como el punto P2(x2, y2) , entonces satisface su ecuación

La ecuación (3) se conoce como la forma: DOS-PUNTOS de la ecuación de la recta.
Ecuación segmentaría de la línea recta
Considere la recta l de la cual conocemos los interceptó a y b con los ejes x e y respectivamente

Como l pasa por los puntos A(a, 0) y B(0, b), entonces de acuerdo a la sección la ecuación de l viene dada por:

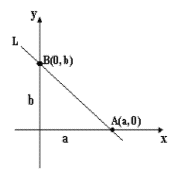
Dividiendo esta última ecuación por b, se obtiene:

La ecuación (1) se conoce como la ecuación SEGMENTARIA, CANÓNICA O FORMA DE LOS INTERCEPTOS de la línea recta. Los números a y b son las medidas de los segmentos que la recta intercepta con cada eje, con su signo correspondiente, pues haciendo en (1)
y = 0, resulta x = a (Intercepto con el eje x)
x = 0, resulta x = b (Intercepto con el eje y)
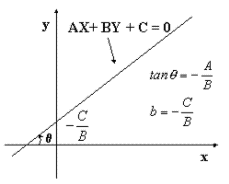
Ecuación general de la línea recta
.... La ecuación Ax + By +C = 0 donde A, B, C son números reales y A, B no son simultáneamente nulos, se conoce como la ECUACIÓN GENERAL de primer grado en las variables x e y. 
..La ecuación explícita de la recta cuando se conocen dos puntos excluye las rectas paralelas al eje y, cuyas ecuaciones son de la forma x = constante, pero todas las rectas del plano, sin excepción, quedan incluidas en la ecuación Ax + By + C = 0 que se conoce como: la ecuación general de la línea recta, como lo afirma el siguiente teorema
TEOREMA
La ecuación general de primer grado Ax + By + C = 0 (1) , R; A y B no son simultáneamente nulos, representan una línea recta.

Demostración
 i.   Se puede Considerar varios casos:
A = 0, B diferente de 0.
       En este caso, la ecuación (1) se transforma en By + C = 0,0de donde

La ecuación (2) representa una línea recta paralela al eje x y cuyo intercepto con el eje y es 
ii. En este caso, la ecuación (1) se transforma en Ax + C = 0, de donde

La ecuación (3) representa una línea recta paralela al eje y y cuyo intercepto con el eje x es 
iii. En este caso, la ecuación (1) puede escribirse en la siguiente forma:

La ecuación (4) representa una línea recta, cuya pendiente es  y cuyo intercepto con el eje y viene dado por 
observaciones

    i.   Es posible escribir la ecuación general de la línea recta en varias formas, de tal
         manera que solo involucre dos constantes. Es decir, si A, B y C son todos distintos
         de cero, podemos escribir la ecuación (1), en las siguientes formas equivalentes:
    
En cada una de las ecuaciones (1A), (1B) y (1C) existe esencialmente solo dos

        constantes independientes, por ejemplo  en (1A)

Esto indica que para determinar la ecuación de una recta en particular, necesitamos conocer dos condiciones, como por ejemplo, dos puntos, un punto y la pendiente, en concordancia con lo establecido en los numerales anteriores.
iii.   Cuando la ecuación de una recta esta expresada en la forma general
          Ax + By + C = 0, su pendiente ó coeficiente angular con respecto al eje x, m
         viene dado por y su coeficiente angular n, con respecto al eje y

         viene dado por  .
    
   Los coeficientes A y B se denominan coeficientes directores de la recta.
IV. Historia del Cálculo
          DE CÓMO SE GESTÓ Y VINO AL MUNDO EL CÁLCULO INFINITESIMAL

N e w t o n               L e i b n i z

( 1 642 - 1 727 )           ( 1 646 - 1 716)

     Del legado de las matemáticas, el cálculo infinitesimal es, sin duda, la herramienta más potente y eficaz para el estudio de la naturaleza. El cálculo infinitesimal tiene dos caras: diferencial e integral; y un oscuro interior donde, como demonios, moran los infinitos: grandes y pequeños. Los orígenes del cálculo integral se remontan, como no, al mundo griego; concretamente a los cálculos de áreas y volúmenes que Arquímedes realizó en el siglo III a.C. Aunque hubo que esperar mucho tiempo, hasta el siglo XVII, ¡2000 años!, para que apareciera -o mejor, como Platón afirmaría, para que se descubriera- el cálculo. Varias son las causas de semejante retraso.
Entre ellas debemos destacar la inexistencia de un sistema de numeración adecuado -en este caso el decimal- así como del desarrollo del álgebra simbólica y la geometría analítica que permitieron el tratamiento algebraico -y no geométrico- de las curvas posibilitando enormemente los cálculos de tangentes, cuadraturas, máximos y mínimos, entre otros. Todo ello ocurrió principalmente en el siglo XVII.

Ya los griegos se habían preocupado de como tratar ese ente tan curioso -como difícil- que es el infinito. Para los griegos el infinito aparece de dos maneras distintas: lo infinitamente pequeño y lo infinitamente grande. Ya se vislumbra de algún modo en la inconmensurabilidad de la diagonal del cuadrado; también, claro está, lo tenemos en la famosa paradoja de Zenón sobre Aquiles y la tortuga, por ello no es de extrañar que alguien intentara regularlos.
Ese alguien fue Aristóteles. Lo que hizo fue prohibir el infinito en acto "no es posible que el infinito exista como ser en acto o como una substancia y un principio", escribió, pero añadió "es claro que la negación absoluta del infinito es una hipótesis que conduce a consecuencias imposibles" de manera que el infinito "existe potencialmente [...] es por adición o división". Así, la regulación aristotélica del infinito no permite considerar un segmento como una colección de puntos alineados pero sí permite dividir este segmento por la mitad tantas veces como queramos. Fue Eudoxio, discípulo de Platón y contemporáneo  de Aristóteles quien hizo el primer uso "racional" del infinito en las matemáticas. Eudoxio postuló que "toda magnitud finita puede ser agotada mediante la substracción de una cantidad determinada". Es el famoso principio de Arquímedes que éste toma prestado a Eudoxio y que sirvió a aquél para superar la primera crisis de las Matemáticas -debida al descubrimiento de los irracionales-.
No obstante, fue Arquímedes el precursor del cálculo integral aunque desgraciadamente su método se perdió y por tanto no tuvo ninguna repercusión en el descubrimiento del cálculo -recordemos que su original método "mecánico" donde además se saltaba la prohibición aristotélica de usar el infinito in acto se perdió y solo fue recuperado en 1906 ... La genial idea del siracusano fue considerar las áreas como una colección -necesariamente infinita- de segmentos. Habrá que esperar 2000 años hasta que otro matemático -en este caso Cavalieri- volviera a usar de esa manera los infinitos. De hecho Leibniz descubrió la clave de su cálculo al ver un trabajo de Pascal donde éste usaba un método semejante.
      La necesidad de entender obras griegas difíciles como las de Arquímedes tuvo gran influencia en el nacimiento del cálculo. -ya en el siglo XVII se habían recuperado y se dominaban la mayoría de las obras griegas.
También ayudó al surgimiento del cálculo el cambio de actitud en la matemática del siglo XVII quizá influenciada por los grandes descubrimientos de todo tipo -geográficos, científicos, médicos y tecnológicos- que fue el interés de los matemáticos por descubrir más que por dar pruebas rigurosas. Ello potenció sin duda el uso del infinito sin las limitaciones aristotélicas. Y finalmente, el descubrimiento de la Geometría analítica de Descartes y Fermat.
La primera parte del siglo XVII vio el nacimiento de la geometría analítica de Fermat y Descartes. La importancia de este descubrimiento consiste en que la geometría analítica permite el tratamiento algebraico de problemas geométricos, al asignar a las curvas, superficies, etc. fórmulas algebraicas que las describen y permiten su manipulación analítica. De esta forma encontrar tangentes, por ejemplo, se hacía extremadamente sencillo -basta saber calcular las derivadas como ahora sabemos- frente a los engorrosos, y específicos para cada curva,  procedimientos geométricos.
      Como ya mencionamos, en el siglo XVII los matemáticos perdieron el miedo  a los infinitos que los griegos les habían tenido: Kepler y Cavalieri fueron los primeros en usarlos, empezaron a andar un camino que llevaría en medio siglo al descubrimiento del cálculo infinitesimal. El primer paso importante se debe a Cavalieri -discípulo de Galileo-. Cavalieri considera áreas formadas por segmentos y volúmenes formados por trozos de áreas planas redescubriendo las bases metodológicas del método mecánico -y desconocido en aquella época- de Arquímedes. Cavalieri incluso fue más allá intentando construir una teoría de indivisibles que le permitiera, evitando los infinitos, demostrar rigurosamente sus resultados -cosa que no consiguió ya que el infinito en acto siempre acababa apareciendo en alguna parte-.  Las desventajas de su método de indivisibles -poca generalidad, debilidad lógica, excesivos razonamientos y procedimientos geométricos- fueron rápidamente superados por Torricelli, Fermat, Pascal, Wallis y Roberval.

Otro de los protagonistas de nuestra historia es, sin duda, Grégoire de Saint-Vicent, jesuita discípulo de Clavius. Sus principales aportaciones las publicó en su Opus geometricum. En ella desarrolla un método de integración geométrico, estudia las series geométricas incluyendo diversas aplicaciones de las mismas discutiendo, como no, la conocida aporía de Zenón sobre Aquiles y la tortuga que además resolvía magistralmente argumentando que Zenón no consideró en la persecución de Aquiles que el tiempo formaba una progresión geométrica de razón 1/2 y por tanto tardaba un tiempo finito en alcanzar a la tortuga. Una de las aportaciones más valiosas de Saint-Vicent consistió en su hallazgo de que el área encerrada bajo una hipérbola se expresaba mediante los logaritmos.
Nuestro próximo personaje es John Wallis, miembro fundador de la Royal Society de Londres y editor de obras de Arquímedes que además escribió una Gramática inglesa. Wallis aritmetizó los indivisibles de Cavalieri asignándoles valores numéricos convirtiendo de esta forma el cálculo de áreas -hasta el momento algo meramente geométrico- en cálculos aritméticos más un primitivo proceso de límite haciendo además un uso "descarado" del infinito -a él debemos también el símbolo que usamos actualmente, ese 8 acostado-.
Es curiosa la opinión que él mismo profesaba de sus métodos: "Este procedimiento es altamente heterodoxo, pero puede verificarse mediante el bien conocido método de figuras inscritas y circunscritas, lo que es superfluo, porque la frecuente iteración produce náuseas al lector. Cualquier ducho en la materia puede realizar la prueba", escribió en su Arithmetica infinitorum. Usando su método aritmético, la inducción incompleta,  y su intuición llegó a calcular el área de todas las parábolas generalizadas x ^ r con r racional excluyendo al 1, además de una bellísima fórmula para calcular Pi.
El trabajo de Wallis influyó enormemente en Newton quien aseguró que el desarrollo del binomio y otras ideas iniciales sobre el cálculo se originaron en su estudio del libro de Wallis en la época de estudiante en Cambridge.
El mismo Wallis propone una genealogía del cálculo:
Método de exhausión (Arquímedes)
Método de los indivisibles (Cavalieri)
Aritmética de los infinitos (Wallis)
Métodos de las series infinitas (Newton)
     Dediquemos algún tiempo a comentar los métodos infinitesimales relacionados con el cálculo de tangentes, que junto al de áreas constituyeron la base del cálculo. En la parte central del siglo XVII, las cantidades infinitesimales, los fantasmas de cantidades desaparecidas, como alguien las llamó en el siglo XVIII, fueron cada vez más usadas para resolver problemas de cálculos de tangentes, áreas, volúmenes, etc.; los primeros darían origen al cálculo diferencial, los otros al integral.  Como hemos mencionado Saint Vincent, Pascal, Wallis, ... siguieron los pasos de Kepler y Cavalieri; además de los infinitésimos cada vez se usaban más fórmulas y menos dibujos: la geometría analítica cumplía su función de puente entre la geometría y el análisis. Si Isaac Barrow, el maestro de Newton en Cambridge la hubiera estudiado bien, podría haber arrebatado a su discípulo el descubrimiento del cálculo. En efecto, la geometría analítica amplió considerablemente el horizonte de las curvas geométricas. Este incremento de nuevas curvas hizo imprescindible el desarrollar nuevos métodos para calcular tangentes.  Uno de ellos fue el método de adigualdades de Pierre Fermat que servía además para calcular máximos y mínimos. Esto unido a sus trabajos sobre cuadraturas le hacen merecedor a un puesto de honor como precursor del cálculo. Newton, en una carta descubierta en 1934, escribió en relación con sus ideas para el desarrollo del cálculo: "La indicación me la dio el método de Fermat para las tangentes. Aplicándolo a las ecuaciones abstractas directa e inversamente, yo lo hice general".
Relacionado con los problemas de tangentes surgió a mediados del S.XVII el llamado problema inverso de tangentes, es decir, deducir una curva a partir de las propiedades de sus tangentes. El primero en plantear un problema de este tipo fue Florimond de Beaune, discípulo de Descartes, quien planteó, entre otros, el problema de encontrar la curva con subtangente constante. El propio Descartes lo intentó sin éxito siendo Leibniz el primero en resolverlo en la primera publicación de la "historia sobre el cálculo infinitesimal". De hecho un elemento esencial para el descubrimiento del cálculo fue el reconocimiento de que el problema de las tangentes y las cuadraturas eran problemas inversos; es por eso que la relación inversa entre la derivación y la integración es lo que hoy llamamos Teorema fundamental del cálculo.
     Newton en su célebre frase "Si he llegado a ver más lejos que otros es por que me subí en hombros de gigantes" se refiere entre otros a su maestro y mentor Isaac Barrow. Barrow fue probablemente el científico que estuvo más cerca de descubrir el cálculo. Llegó a las matemáticas en su afán de comprender la teología -de hecho se marchó de su cátedra en Cambridge, cediéndosela a Newton para continuar sus estudios teológicos-. En la lección X de su obra Letiones opticae & geometricae Barrow demuestra su versión geométrica del Teorema fundamental del cálculo.
       En el último cuarto del siglo XVII, Newton  y Leibniz, de manera independiente, sintetizaron de la maraña de métodos infinitesimales usados por sus predecesores dos conceptos, los que hoy llamamos la derivada y la integral, desarrollaron unas reglas para manipular la derivada -reglas de derivación- y mostraron que ambos conceptos eran inversos- Teorema fundamental del cálculo-: acababa de nacer el cálculo infinitesimal. Para resolver todos los problemas de cuadraturas, máximos y mínimos, tangentes, centros de gravedad, etc. que habían ocupado a sus predecesores bastaba echar a andar estos dos conceptos mediante sus correspondientes reglas de cálculo.
El primero en descubrirlo fue Newton, pero su fobia por publicar le hizo guardar casi en secreto su descubrimiento. Newton gestó el cálculo en sus anni mirabilis (1665-1666) cuando se refugiaba en su casa materna de la epidemia de peste que asolaba Inglaterra. De hecho su primera obra  sobre el cálculo, De analyse per aequationes numero terminorum infinitas -que le valió la cátedra lucasiana que dejó su maestro Barrow- fue finalizada en 1669 aunque sólo la publicó en 1711. La segunda obra de Newton sobre el cálculo fue escrita dos años más tarde en 1671 pero esperaría hasta 1737 para ver la luz !diez años después de su muerte y 66 después de escrita!. Se trata de De methodis serierum et fluxionum.

En ella Newton describe sus conceptos de fluente -es una variable en función del tiempo- y fluxión de la fluente -la derivada respecto al tiempo de la fluente- como entidades propias, con unas reglas algorítmicas de fácil uso que luego usará para resolver distintos problemas de máximos y mínimos, tangentes, cuadraturas -en relación a este último, estableció el ya mencionado Teorema fundamental del cálculo-. Para demostrar la potencia de su cálculo Newton se dedica en unas "pocas" páginas a resolver todos los problemas de cálculo de tangentes, áreas, etc. que habían ocupado a sus predecesores.
Una pregunta que casi inmediatamente aflora en la mente es ¿por qué Newton tardó tanto en publicar sus resultados? A parte de su peculiar personalidad y las distintas disputas que tuvo con muchos de sus contemporáneos, Newton era consciente de la débil fundamentación lógica de su método de cálculo de fluxiones -no obstante siempre hubo copias de sus trabajos circulando entre sus amigos-.
Este temor también está patente en su obra cumbre: Los Principia, donde optó por un lenguaje geométrico más riguroso -y oscuro- eliminando todo indicio de su cálculo que probablemente usó -se puede encontrar una única mención del mismo en el lema II de la sección II del libro II: la regla para derivar productos-.

     Leibniz, más conocido como filósofo, fue el otro inventor del cálculo. Su descubrimiento fue posterior al de Newton, aunque Leibniz fue el primero en publicar el invento. Lo hizo además usando una vía ciertamente novedosa en aquella época: para facilitar la difusión de sus resultados los publicó en una de las recién creadas revistas científico filosóficas, el Acta Eroditorum, que el mismo había ayudado a fundar -eran ciertamente momentos importantes para la ciencia donde empezaron a aparecer las revistas científicas que permitirían luego y hasta nuestro días la difusión del conocimiento y los descubrimientos científicos-. Durante una estancia en París -ya que era un afamado diplomático- Leibniz conoce a Huygens quien le induce a estudiar matemáticas.
En 1673, luego de estudiar los tratados de Pascal, Leibniz se convence que los problemas inversos de tangentes y los de cuadraturas eran equivalentes. Alejándose de estos problemas, a partir de sumas y diferencias de sucesiones comienza a desarrollar toda una teoría de sumas y diferencias infinitesimales que acabarían en la gestación de su cálculo por el año 1680 y a diferencia de Newton si lo publica en las mencionadas Actas con el título "Un nuevo método para los máximos y los mínimos, así como para las tangentes, que no se detiene ante cantidades fraccionarias o irracionales, y es un singular género de cálculo para estos problemas". En este artículo de 6 páginas -e incomprensible como él mismo luego reconoce- Leibniz recoge de manera esquemática sin demostraciones y sin ejemplos su cálculo diferencial -"un enigma más que una explicación" dijeron de él los hermanos Bernoulli.

También Leibniz resuelve el ya mencionado problema de De Beaune encontrando que la solución era el logaritmo. El siguiente artículo de Leibniz se llamó "Sobre una geometría altamente oculta y el análisis de los indivisibles e infinitos", también publicado en las Actas Eroditorum en 1686. En él aparece por primera vez la notación para la integral que todavía hoy usamos -en el primero introduce la notación "dx" para la diferencial-.
     Como colofón a estas páginas dedicaremos unas líneas a tratar la mayor de todas las disputas que ha conocido la ciencia: la prioridad de la invención del cálculo. Las suspicacias entre Newton y Leibniz y sus respectivos seguidores, primero sobre quién había descubierto antes el cálculo y, después, sobre si uno lo había copiado del otro, acabaron estallando en un conflicto de prioridad que amargó los últimos años de ambos genios. Para comenzar diremos que la disputa fue evitable pues los métodos de ambos genios tienen importantes diferencias conceptuales que indican claramente la génesis independiente de los mismos. Newton consideraba las curvas generadas por el movimiento continuo de un punto basándose su cálculo diferencial en la medida de la variación de la misma -de su fluir- mientras que Leibniz consideraba una curva como formada por segmentos de longitud infinitesimal cuya prolongación generaba la tangente en cada punto y de cuya geometría se obtiene la correspondiente relación entre las diferenciales. Incluso la fundamentación de ambos métodos es totalmente distinta. Si el de Newton fue resuelto totalmente mediante el concepto de límite, el de Leibniz tuvo que esperar hasta la década 1960-70 hasta la aparición del Análisis no-estándard de Abrahan Robinson.
La polémica en cuestión se fraguó a finales del siglo XVII: por un lado Leibniz no había hecho ninguna alusión al cálculo infinitesimal de Newton -que el mismo Newton le había indicado que existía en sus Epistolae : Expistola prior  y posterior, sendas cartas dirigidas a Leibniz. En ambas Newton explica muy someramente -básicamente se centra en el teorema del binomio- su método de cálculo.- Además en Holanda -como le aseguró Wallis a Newton- se atribuía el cálculo a Leibniz, eso sin contar que los discípulos de Leibniz habían publicado el primer libro sobre el cálculo: el Analyse des infiniment petits que redactó el Marquéz de L'Hospital a partir de las clases particulares que le dio Juan Bernoulli.
 
La respuesta de los seguidores de Newton no se hace esperar. Primero el propio Newton hace publicar en el tercer volumen de las obras matemáticas de Wallis la correspondencia cursada con Leibniz, las Epistolas prior y posterior donde éste pedía a Newton le enviase resultados sobre series, luego Fatio de Duillier, amigo de Newton, acusa a Leibniz de haber plagiado a Newton y como no, en su ya mencionada De quadratura curvarum, Newton alega "En una carta escrita al Sr. Leibniz en 1676 y publicada por Wallis, mencionaba un método por el cual había encontrado algunos teoremas generales acerca de la cuadratura de figuras curvilíneas [...] Hace años presté un manuscrito conteniendo tales teoremas; y habiéndome encontrado desde entonces con varias cosas copiadas de él, lo hago público en esta ocasión". La respuesta de Leibniz no se hizo esperar.
En una reseña del De quadratura curvarum, publicada anónimamente -aunque era fácil reconocer a su autor: Leibniz - en 1705 en las Actas se dice "Para entender mejor este libro los siguientes hechos deben ser conocidos. Cuando una cantidad varía continuamente como, por ejemplo, una línea varía por el fluir de un punto que la describe, aquellos incrementos momentáneos son llamados diferencias [...] Y por tanto ha aparecido el cálculo diferencial y su converso, el cálculo sumatorio. Los elementos de este cálculo han sido publicados por su inventor el Dr. Gottfried Wilhelm Leibniz en estas Actas, y sus varios usos han sido mostrados por él y por los Drs. y hermanos Bernoulli y por el Dr. Marquéz de L'Hospital. En vez de las diferencias leibnizianas, el Dr. Newton empleó, y ha empleado siempre, fluxiones". Esta reseña fue el detonante del mayor ataque contra Leibniz desde las Philosophical Transactions firmado por John Keill quien acusa abiertamente a Leibniz de plagio. Tras la protesta de Leibniz la Royal Society nombra una comisión -que resultó estar plagada de amigos de Newton - que luego de varias deliberaciones dictaminó que Newton fue el primero y no acusó a Leibniz - aunque tampoco rectificó las duras palabras de Keill-. Esta absurda guerra duró hasta principios del siglo XIX cuando finalmente los matemáticos ingleses deciden adoptar la notación leibniziana, que hasta el momento habían ignorado.

     Como apéndice a nuestra exposición vamos a relatar, a modo de realzar la gran potencia del cálculo, uno de los problemas que se resolvió gracias a la nueva herramienta descubierta por Newton y Leibniz: el problema de la braquistocrona. El problema consistía en determinar la curva por la que un cuerpo desciende en el menor tiempo posible entre dos puntos que no estén en posición vertical u horizontal. Este problema ya interesó en su día a Galileo aunque éste fue incapaz de resolverlo -lo cual no es raro pues para ello se precisaba del cálculo-. La historia es como sigue.
En el número de junio de 1696 de las Actas Eroditorum, Juan Bernoulli lanzó un reto a los mejores matemáticos del mundo. En realidad era un reto encubierto a Newton. Al cabo del año -el plazo original fue de seis meses pero a petición de Leibniz se amplió para que tuvieran tiempo los matemáticos franceses e italianos que se habían enterado tarde- aparecieron cinco soluciones: una de Leibniz,  una del mismo Juan Bernoulli, otra de su hermano Jacobo Bernoulli, una del Marquéz de L'Hospital y una anónima. Todas, excepto la de L'Hospital daban con la solución: la cicloide. ¿Quién era ese autor anónimo que escogió las Philosophical Transactions para publicar su genial solución que sólo contenía 67 palabras?. Un vistazo a la solución fue suficiente para que Juan Bernoulli exclamara "tanquam ex ungue leonen", algo así como "¡reconozco al león por sus garras!" pues claro está que era Newton. Años más tarde se aclaró toda la historia. Como ya dijimos el reto estaba dirigido a los matemáticos ingleses y a Newton en particular justo en el momento en que comenzaba la polémica sobre la prioridad para ver si el cálculo de Newton era tan bueno y poderoso para resolverlo. Además, en una carta de Leibniz a Juan Bernoulli éste conjetura que sólo quien conozca el cálculo podrá resolverlo -Newton entre ellos claro está-. Como no podía ser de otra forma el reto llegó a Newton aunque por aquel entonces ya no "hacía ciencia" sino que trabajaba en la Casa de la Moneda inglesa. Según cuenta la sobrina de Newton, este recibió el problema a las 4 de la tarde cuando regresó cansado de la Casa de la Moneda y tenía lista su solución 12 horas después -aunque lo que probablemente no sabía la sobrina era que Newton ya había pensado en ese problema unos años antes y que casi seguro lo había resuelto por lo que sólo tuvo que refrescar la memoria ese día-. Nuevamente aparece la misma pregunta: Si Newton ya había resuelto el problema ¿por qué no lo publicó? Como respuesta final a esta pregunta tomaremos la que dió Augusto de Morgan "Cada descubrimiento de Newton tenía dos aspectos. Newton tuvo que hacerlo y, luego, los demás teníamos que descubrir que él lo había hecho"
 

V. Definición del calculo vectorial

El cálculo vectorial es un campo de las matemáticas referidas al análisis real multivariable de vectores en 2 o más dimensiones. Consiste en una serie de fórmulas y técnicas para solucionar problemas muy útiles para la ingeniería y la física.
Consideramos los campos vectoriales, que asocian un vector a cada punto en el espacio, y campos escalares, que asocian un escalar a cada punto en el espacio. Por ejemplo, la temperatura de una piscina es un campo escalar: a cada punto asociamos un valor escalar de temperatura. El flujo del agua en la misma piscina es un campo vectorial: a cada punto asociamos un vector de velocidad.
Cuatro operaciones son importantes en el cálculo vectorial:

• Gradiente: mide la tasa y la dirección del cambio en un campo escalar; el gradiente de un campo escalar es un campo vectorial.

• Rotor o rotacional: mide la tendencia de un campo vectorial a rotar alrededor de un punto; el rotor de un campo vectorial es otro campo (seudo)vectorial.

• Divergencia: mide la tendencia de un campo vectorial a originarse en o a converger hacia ciertos puntos; la divergencia de un campo vectorial es un campo escalar.

• Laplaciano

La mayoría de los resultados analíticos se entienden más fácilmente usando la maquinaria de la geometría diferencial, de la cual el cálculo vectorial forma un subconjunto.